Hi Friends!
I am looking for an example program how do draw an astrology chart with Allegro. I mean something like this:

Which chart, specifically? They all have geometric differences in those pictures.
It doesn't look too hard at first glance. The worst part would be getting the math to center text between the lines.
Are you looking to have a variable number of divisions? For example, this one is:
{"name":"astrology-wheel.gif","src":"\/\/djungxnpq2nug.cloudfront.net\/image\/cache\/1\/4\/14dcab44d320af2035eb9a3ec16feda5.gif","w":2064,"h":2070,"tn":"\/\/djungxnpq2nug.cloudfront.net\/image\/cache\/1\/4\/14dcab44d320af2035eb9a3ec16feda5"}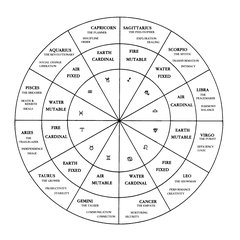
subdivides at 30/60/90 degree intervals. I mean, all of them are 12-month calendars, obviously. But are you looking for a generic case code?
Another one has much more stuff in it:
{"name":"teachingwheel.jpg","src":"\/\/djungxnpq2nug.cloudfront.net\/image\/cache\/5\/f\/5ff53e8572562c69916343289c7ed594.jpg","w":480,"h":480,"tn":"\/\/djungxnpq2nug.cloudfront.net\/image\/cache\/5\/f\/5ff53e8572562c69916343289c7ed594"}
And wrapped/angled text plus background textures and so on. It's also rotated 15 degrees.
Thanks for your reply, Chris!
I think i would need a generic case code, as there are a few circles needed:
1. The background diagram with 12 equal divisions, but rotated, so that the ascendant is always at the outer left edge.
2. Signs in right positions.
3. Planet symbols in the inner circle.
4. Aspect lines between the planets.
5. Houses with unequal divisions.
All together it would look like this one:
http://www.astrodreamadvisor.com/How_To_Astrology_Chart.html

What are you wanting to use it for?
Do you just want to generate an image or something more interactive?
Any reason you're wanting to use Allegro and not, say, CSV or something else?
What means CSV? Honestly, my english is still not good enough to participate in the discussions here for more than a few simple words. Go and try to discuss in a german programmer forum in german and you will see how difficult it is.
Special features of my program will be to use more Kuiper Belt Objects, planetoids and aspects like quintile and septile.
Mainly i want to create a program for my personal use. And if i would want to sell it, what would be the conditions? (In simple words, please.)

CSV
EEeeerrpps!  Not CSV, I meant to say SVG.
Not CSV, I meant to say SVG.
You can have SVG images in browsers, like PNG. Except with SVG, you can "draw" the image by using HTML or Javascript.
An example: http://www.w3schools.com/svg/svg_inhtml.asp
my english is still not good
Thanks, I'll keep that in mind. 
Maybe a good idea to use SVG, i have thought to save graphics in JPG or GIF before. 
If you draw to an HTML <canvas>, you can right-click and save that as a PNG.
Here is a part of code i found in Pullens "Astrolog" from here:
http://www.astrolog.org/astrolog/astfile.htm
But after all, the graphics output of this program is not very good, so i decided to do it new with Allegro. 